1. 概述
对于绝大多数语言而言,基本上都会有整数、浮点数、字符串和二进制串这几种数据类型,但在计算机系统中,如果追溯到最底层,这些不同种类的信息的表示,都会归结为最简单的01串的有限组合:
01010101010100101010101011111110001111110000111111100011110001
在最底层的计算机硬件实现里,1一般会用一个高电平表示,而0则会用一个低电平表示,回忆一下大学里学的随便一个简单的电子芯片,比如3-8译码器你去翻它的Datas sheet,就会在最底层的计算机硬件里,发现01的真实身份就是一个个具体的电信号,信息的存储、传送、加工,最终、也是最真实的面目就是这些电信号流在CPU、内存、外存、乃至网络中的游走、转移和各种位级的运算,这些底层的电信号的活动,被一层层的抽象、汇聚成更高级、也更复杂的计算机软硬件理论及知识体系。
深入理解计算机系统这本书的最终目的就是这些01串所组成的大千世界的具体轮廓给讲清楚,其方式是最简单的至底向上的逐层讲解。而在本章关注的是最底层的01信号具体是如何抽象表示更高一层的各种基础数据类型和基础数据操作的。
本章共5小节,除去最后一小节的总结内容,前四节分别介绍了信息存储、整数表示、整数运算和浮点数,从全章的目录来看,本章的内容非常清晰,就是计算机底层的01串是如何存储、如何表示的。更数学一点的概括,就是介绍了几个转换函数,输入是计算机所擅长的01二进制串,输出是我们所熟悉的十进制数,以及如何通过位级的算术计算以及逻辑操作来模拟实现十进制数中的算术计算以及逻辑操作。这几种函数的特点是:
- 输入都是
01二进制串 - 输出则是符合各种意义和模式的
基础数据类型
函数体如下:本章的内容就是介绍了这么几种转换函数$ f(x)$。2. 信息的表示所带来的问题
在讲具体的函数之前,首先要明白信息是如何在计算机中存储的:几乎所有的计算使用8位的块(byte,以后统称为字节),作为最小的可寻址的内存单元:
10010110
程序数据、指令和控制信息,都是由这些bytes的组装起来的,对于多字节的数据类型来说,就有一个字节序如何存储和解析的问题:这就是著名的大小端问题:
在将一个多字节表示的程序对象存储到连续的地址空间的时候,我们必然要面临两个问题:
- 这个对象的地址是什么?
- 在内存中如何排列这些字节?
在几乎所有机器上,这两个问题的答案都将是: - 多字节都被存储为连续的字节序列,对象的地址为所使用字节中最小的地址;
- 对于大多数
Intel兼容机都只用小端模式,而许多新的微处理器的大小端是可选的,也即所谓的双端机(bi-endian),比如ARM微处理器,但有意思的是运行于其上的两种最流行的Android和iOS却只能运行于小端模式; - 在网络中进行的传送的
字节序都统一使用大端模式,这是事实上的网络协议簇TCP/IP中明确指定的。
那么为什么TCP/IP协议里规定一定要使用大端法表示网络字节序呢?先不急着回答这个问题,我们先来看看什么是大端和小端。
在本文前面我们提到目前计算机的最小寻址单元是1字节。而大小端问题存在的根本原因就是:
很多基础数据类型的二进制表示的长度超出了计算机的最小寻址单元(1字节 or byte),在存储这些超过最小寻址单元的数据类型的值的时候,就必然要指定拆分后的若干块的存储顺序。
下图列出了C语言声明的基础数据类型在32位计算机和64位计算机上的字节数:
| 数据类型 | 32位计算机系统 | 64位计算机系统 |
|---|---|---|
| [signed] char / unsigned char | 1 | 1 |
| short / unsigned short | 2 | 2 |
| int / unsigned | 4 | 4 |
| long / unsigned long | 4 | 8 |
| int32_t / uint32_t | 4 | 4 |
| int64_t / uint_64 | 8 | 8 |
| char /void / int * … | 4 | 8 |
| float | 4 | 4 |
| double | 4 | 4 |
lihux.me-1 C语言中常见的数据类型及其在不同系统中的字长
当一个数据类型长度大于1最小寻址单元的时候(在C语言中sizeof(type) > 1),如果它的一个值如果要存入内存中,那么1个内存单元显然是不够的,需要将实例进行拆分为sizeof(type)个数据块,每一个数据块存入一个最小寻址单元中。我们以一个简单的32位整形变量的存储来说明问题,为了便于表示,我们采用十六进制:
int32_t dog = 0x99887700
数学常识告诉我们99是最高字节,00是最低字节,这种排列是从左到右按照从高字节到低字节的顺序排列的,这里高字节的高就意味着其拥有更高的权重或者:power。现在假设我们的计算机内存只有4字节,那么这块内存的地址就是0 1 2 3:
因为我们要存储的0x99887700需要占用4 bytes的存储空间(在这里也就是要占满整个内存),那么我们首先要将0x99887700拆分为4块:99、88、77和00。
那么问题来了:该先存入这四块中的哪一个值到内存的第0位呢?
按照我们视觉上从左到右的阅读习惯,我们会很自然的按照99 88 77 00的顺序存储它们:而这就是所谓的大端法(big-endian):高字节存入到底地址(当然你也可以说是:低地址存高字节)

如果按照阿拉伯人的从右到左的阅读习惯,按照00 77 88 99的顺序依次存入内存,这就是所谓的小端法(little-endian):低字节存入到低地址(或者说是:低地址存低字节)。
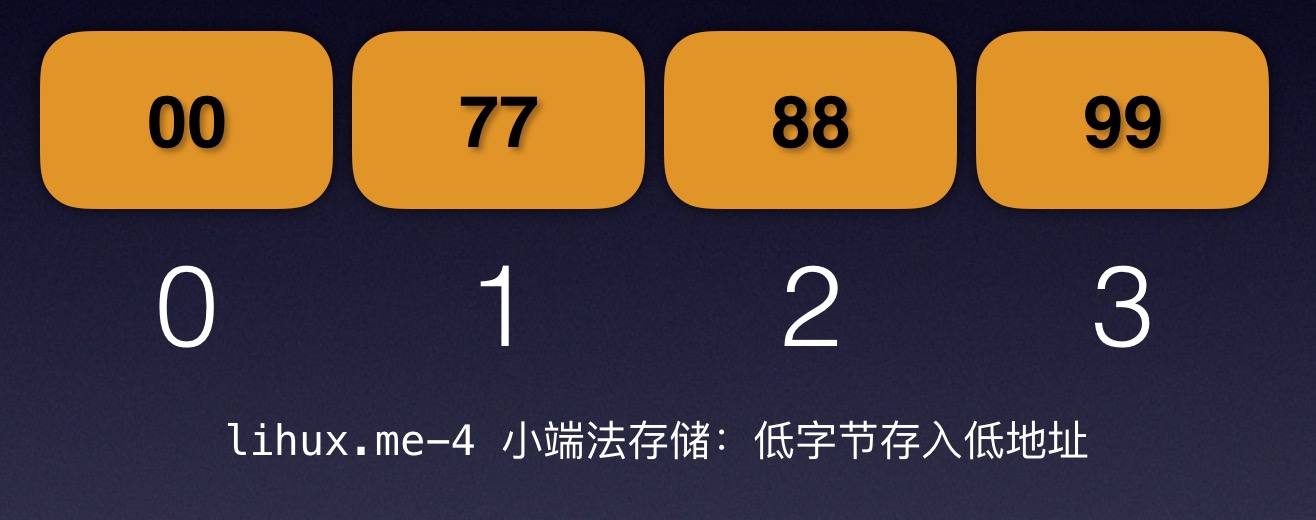
好了,关于大小端,其实就是这么简单。对于机器而言,选择大端还是小端没有优劣之分。
最后的最后,我们可以回答一下开头提出的问题了:为什么TCP/IP协议明确要求选用大端表示呢?
其实,答案很简单:TCP/IP传输的报文为了便于人们阅读(前面提到了绝大部分人的阅读习惯是从左到右的顺序)。关于这一点,在TCP/IP协议的RFC1700中也做了说明:
The convention in the documentation of Internet Protocols is to
express numbers in decimal and to picture data in “big-endian” order
[COHEN]. That is, fields are described left to right, with the most
significant octet on the left and the least significant octet on the
right.
The order of transmission of the header and data described in this
document is resolved to the octet level. Whenever a diagram shows a
group of octets, the order of transmission of those octets is the
normal order in which they are read in English.
我猜要是阿拉伯人发明的TCP/IP协议,他们肯定会选用小端法。
3.整数的表示
先说结论,在C语言中,整数包括无符号整数和有符合整数,在计算机中他们分别采用原码和补码予以表示。再留一个问题:为什么无符号整数要用原码,而有符合整数却要用补码表示呢?
在我们上小学的一二年级的时候,我们的数学世界是非常干净的:没有小数、没有负数,更不用提无理数了,那个时候我们以为仅仅是正整数就足以表达整个世界,后来我们发现,是我们太幼稚了,这个世界太复杂,复杂到必须要造出那么多复杂的数才够用。
计算机世界里的抽象都是对真实世界的模拟,因此这种抽象必须要包含各种复杂的数。
3.1无符号整数(正整数和0)
我们先从最简单(至少是看上去最简单)的整数的表示讲起,我们这里约定计算机世界里用一个32 bit的内存来存放一个整数。我们来看看如何用这32 bit内存空间来存储和表示正整数(也即无符号数)和整数:
图lihux.me-5中每一个小方块代表1 bit,每一个小方块都只可能填充0或者1。那么用这些方块的01组合一共有多少种呢? 答案是$2^{32}$种!
根据前文介绍的,整数的表示,实际上就是定义一个函数,输入为32 位二进制序列(因为这里我们假定只使用32 bit来表示整数),这里我们引入数学中向量的概念来表示这个输入的二进制序列:
那么向量$\vec x $的值一共有$2^{w}, w=32$,因此每一个值都可以实际表示一个整数(或者浮点数),剩下的就是定义编码函数对这些值做映射了:
| $\vec x $ |
|---|
| $[11111111,11111111,11111111,11111111]$ |
| $[11111111,11111111,11111111,11111110]$ |
| $[11111111,11111111,11111111,11111101]$ |
| …… |
| …… |
| …… |
| …… |
| $000000000,00000000,00000000,00000011$ |
| $000000000,00000000,00000000,00000010$ |
| $000000000,00000000,00000000,00000001$ |
| $000000000,00000000,00000000,00000000$ |
lihux.me-6 32位二进制表示的全部集合
如果全部列全,则上面这个表格将会有$2^{32}$列,也即4 294 967 296列!约42.9亿列,马云爸爸的银行卡账户如果用这个32位的整形表示则肯定是要溢出的!^^,年前王健林曾说要先定一个小目标,比如说先赚它一个亿,那对于码农的我来说,我也定个小目标:10年以后,我的银行卡余额要让w位 $\vec x$ 表示的无符号整数产生溢出 ^^,但问题是这个w会是多少呢?
则无符号数的编码函数可以定义为(B2U == Binary to Unsigned Integer):
数学公式的魅力就是非常简洁、精确的表达了某种确定的函数关系,比如上面这个公式,就一行,就说明了一切。但数学公式简洁的同时,却又不够直观,可能有些人看了半天才明白,而另外一些人则始终看不明白^_^。好吧,让我们来直观一些用图说话:
无符号数的编码函数$B2U_w(\vec x)$产生的映射结果是: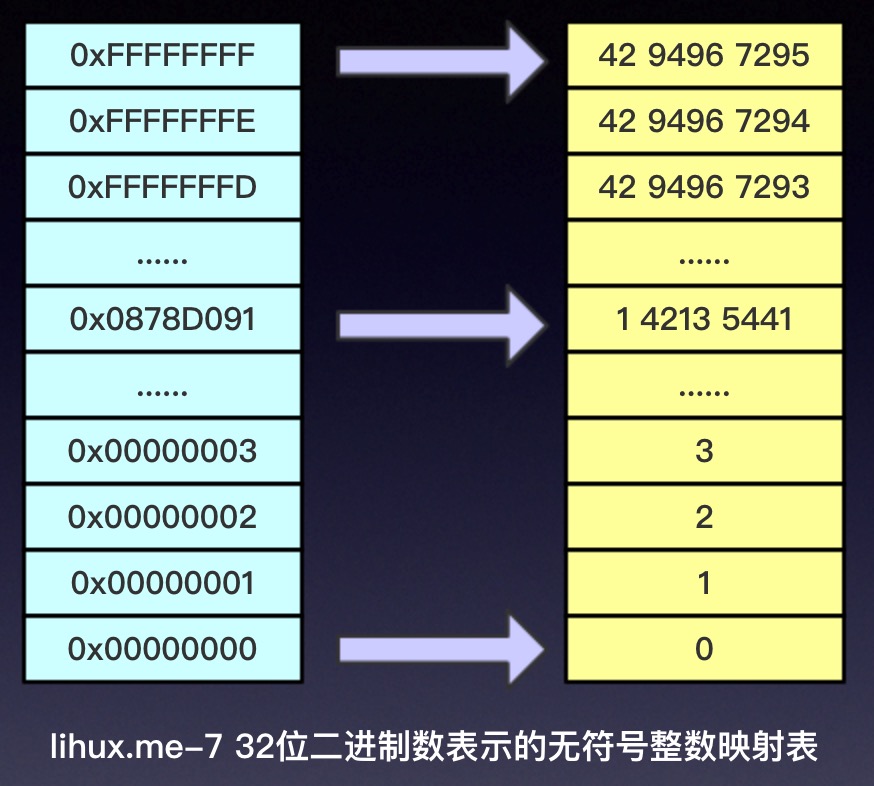
3.整数(负整数、正整数和0)
在上一小节中我们知道,32 bit的二进制序列的所有组合是一个有限集合,集合中元素的个数是 $ 2^{32} $,它所能表示的无符号整数的范围也刚好是$2^{32}$个,那么现在要用这$2^{32}$个元素表示整数,那么显然,依然是只能表示最多$2^{32}$个整数集合,但是整数还包含有负数,那么直觉告诉我们,它所能表示的整数肯定会减半的,事实上也正是如此。不过比较尴尬的是,现在能表示的整数个数是偶数,但我们又刚好又一个0既非正整数,也不是负整数,那么剩下的$2^{32}-1$个元素所能表示的正整数和负整数的个数必然不是相等的(除非0也用两个元素表示,分表为$\stackrel{+}{-}0$,实际上还真有这么表示的),一个为$2^{31}$另外一个为$2^{31}-1$,由此,很自然的我们就能推导出:最大正整数和最大负整数的绝对值是不相等的!。
为了简化我们的整数表示的推演,我们这里讲前面的32 bit二进制流再进一步简化为4 bit,那么在这种情况下,所能表示的无符号整数有0到15,共16个,全部集合见下图: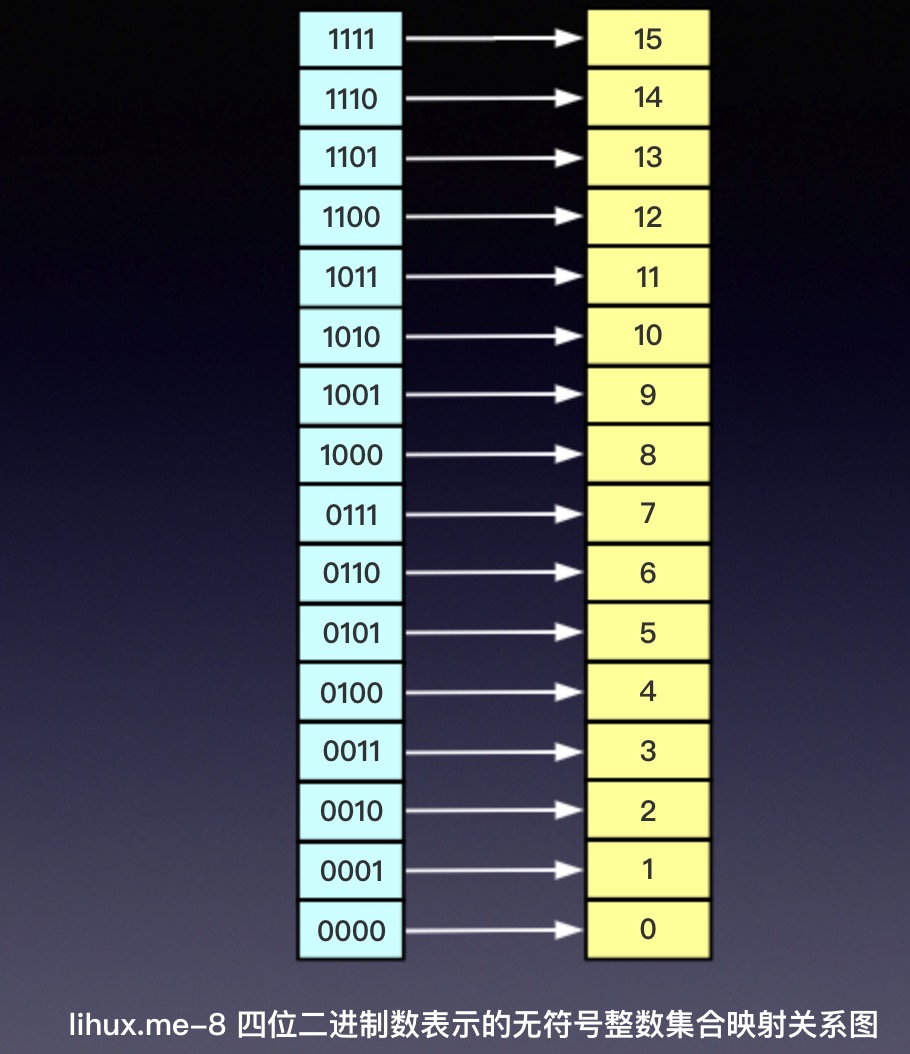
现在我们想要用同样的16个二进制集合表示整数,那么显然我们就被迫要从这表示的无符号整数中挤掉7个或者8个正整数用以表示负整数,那么显然为了保持表示整数值域的连续性,我们剔除掉8~15共8位来表示负数或者-0,但是问题又来了,这剩下的8位该如何表示负数?我们不妨脑洞大开,自己设计一下吧,能想到的至少有四种方案: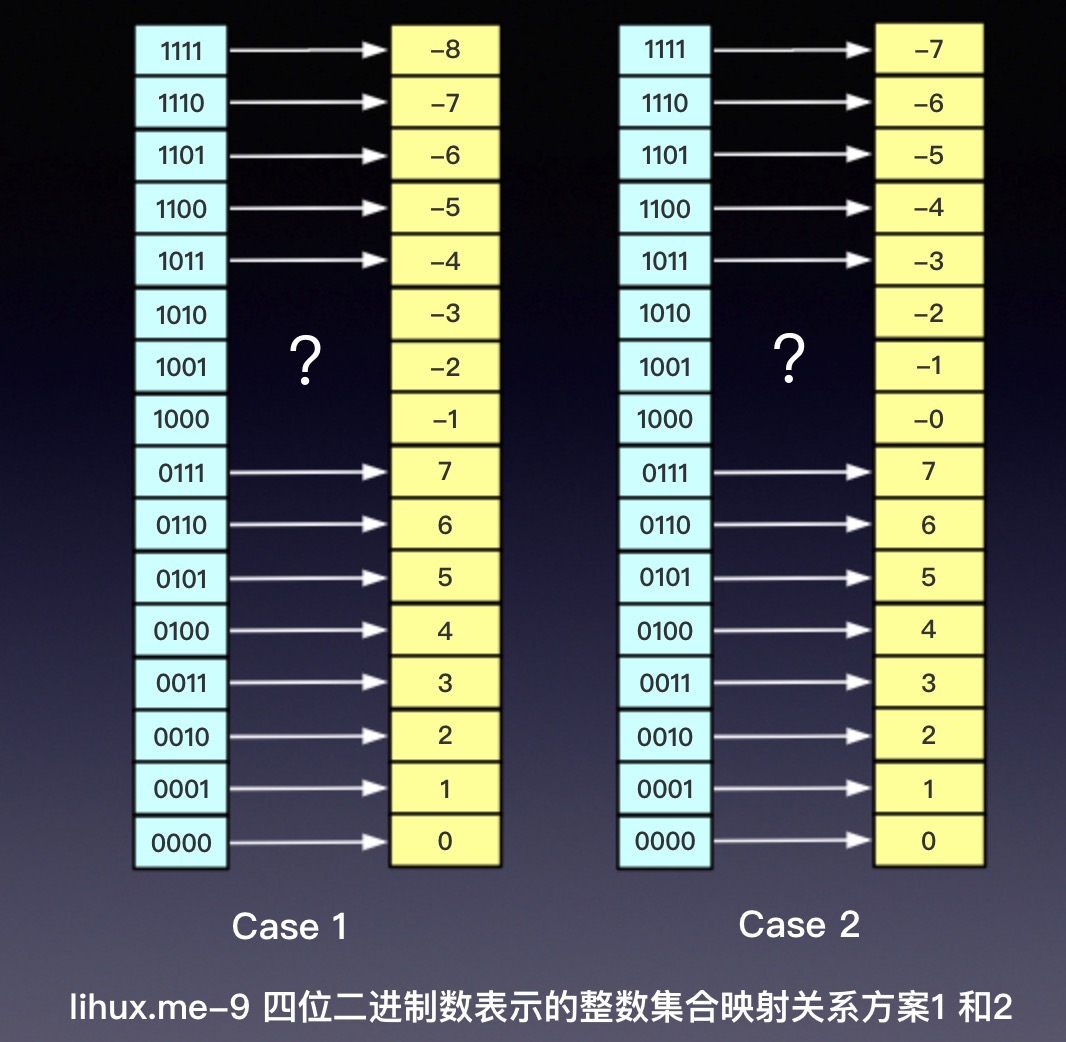
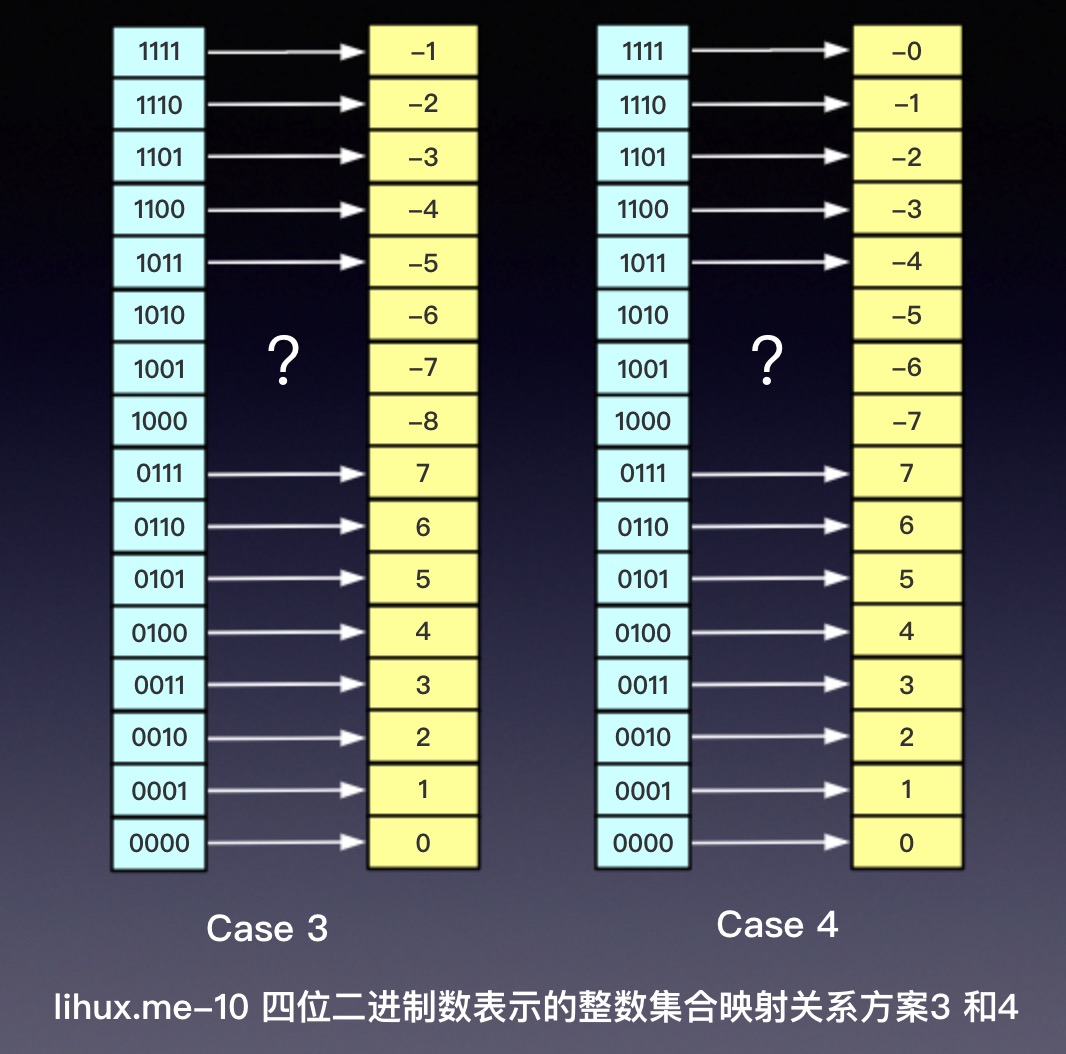
事实上映射方案远不止这些,如果我们让正整数的映射位置不和无符号整数的映射位置保持一致的话,我们还可以这样映射:将无符号整数的映射关系整体上移(-8)如图: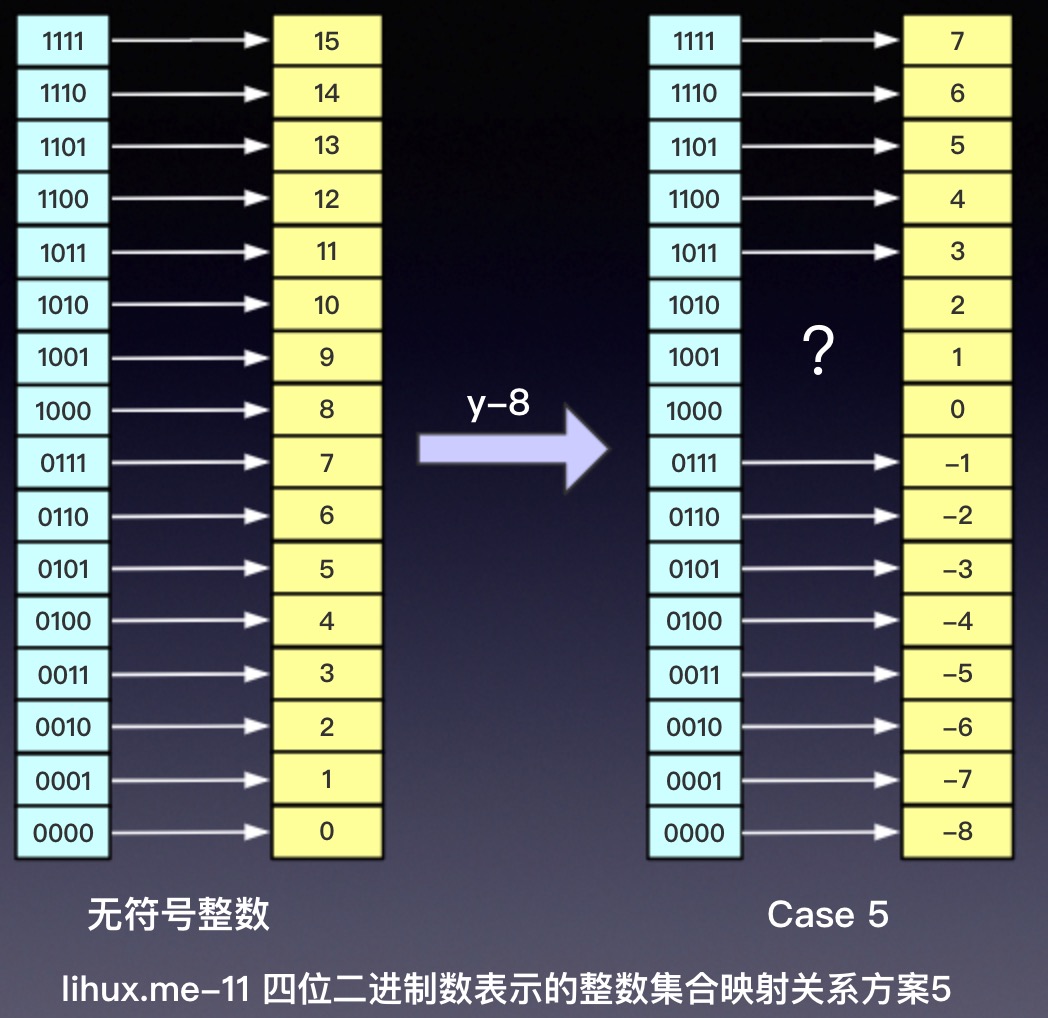
这五种编码方案,我们很容易写出他们的映射函数:
方案1:
方案2:
方案3:
方案4:
方案5:
从数学的角度来看,这五种映射方案都是双射 (bijection),这就保证了 编码的唯一性(双射也称一一映射)。
在这列举的5中方案中,有3套方案(方案2 原码表示、3 反码表示、4 补码表示)是计算机系统中的标准表示方法,但只有补码表示是事实上的标准被几乎所有计算机系统采用:
| Case | 对应命名 | 说明 | 优缺点 |
|---|---|---|---|
| 2 | 原码(Sign-Magnitude) | 整数编码中未采用,浮点数采用 | 正负对称,但是有正负0 |
| 3 | 反码(Ones’Complement) | 过去存在过反码表示的机器,但现在已经绝迹 | 正负对称,但是有正负0 |
| 4 | 补码(Two’s Complement) | 广泛采用,事实上的标准 | 0只有一种表示,但是正负不对称 |
lihux.me-12 计算机系统采用的三种编码方案
那么为什么只有补码会成为计算机系统中整数表示事实上的标准呢?答案就是只有补码能让计算机的算术运算单元ALU按照无符号数的加法来计算补码的加法:即将补码表示的二进制序列看做是无符号数序列,然后对其按照无符号数的加法方法进行相加,得到的结果按照补码的映射规则得到的结果刚好是补码加法应该得到的值!因此,可以认为补码被选中仅仅是因为计算机硬件能够更高效的处理而已。
为了证明这一点,让我们首先来看一张图:如图lihux.me-13所示,我们仍以前文的4 bit整型int4_t值:$x = 2$以及其相反数$y = (-x) = -2$为例,如果我们要计算$ x + y = ?$:
| 编码 | x = 2 | y = -2 | x + y |
|---|---|---|---|
| 原码(Sign-Magnitude) | 0010 | 1010 | 1100 |
| 补码(Two’s Complement) | 0010 | 1110 | 10000(溢出为0000) |
| 反码(Ones’Complement)) | 0010 | 1101 | 1111 |
lihux.me-13 三种编码规则下使用无符号数的加法运算规则计算的值比较
从图中可以很容易的看到:
- 对于原码表示的按照无符号整数的计算结果$1100_2$,根据定义,其最高位是符号位,因而其值转回补码是$-4$,不符合要求;
- 对于补码表示的按照无符号整数的计算结果是$10000_2$,但巧妙的是,最高位发生了溢出,实际得到的结果是$0$,转回补码表示,结果依然是$0$;
- 对于反码表示按照无符号整数的计算结果是$1111_2$,转回反码表示是$-0$,虽然结果正确,但奇葩的是对于$0$它有$+0$何$-0$两种表示,严格意义上并不满足双射。
其实补码和反码的英文名称更能反映出其各自本身的特征:Two’s Complement来自于:对于非负数$x$,我们用$2^w - x$来计算$-x$的表示,这里有一个$2$,所以是Two's;但对于补码,则是用$[111···1]-x$来计算补码表示,这里有很多个$1$,所以是Ones'。
总结一下就是,采用补码表示的有符号整数和采用原码表示的无符号整数,对于计算机的算术运算单元而言,二者都是透明的,它不用去区分不同的编码方式,而只采用一种固定的运算逻辑就能实现两种编码表示的算术运算。计算机执行的整数运算实际上是一种模运算形式,通过溢出来巧妙的使得运算结果符合我们的预期。
4.浮点数:实数在计算机中的表示
首先说明一点,浮点数只是一种计算机表示实数的编码规则的统称,并不是数学世界里的一种数据类型。前面我们讲到,真实的世界中原不止整数一种数据类型那么简单,实数相比整数是一种范围更大、更实用的数据集合。
4.1 固定字长表示实数存在的固有问题
那么问题来了,又是常识告诉我们,浮点数是一个无限集合,而我们的位数固定的二进制序列是一个有限集合,那么我们现在想用一个有限集合映射到一个无限集合上去,显然映射$f(x)$不可能是双射,也就是说浮点数集合中必然有无法从这个有限集合映射得到的元素,更进一步讲,是只有极少数的浮点数能够映射到这个有限集合中,对于32位的系统,我们所能表示的浮点数最多也就只能有$2^{32}$个。这真是一个很悲观的事实。
然而,幸亏,我们常人的一般生活中,对浮点数的要求很有限:我们既不太可能经常使用(绝对值)太过于巨大的浮点数(万万万万亿),也不太可能经常使用(绝对值)太过于微小的浮点数。举例来说,当我们小的时候,夏夜仰望星空的时候,我们一定曾问过我们的妈妈:天上有多少颗星星呢?,妈妈的回答也许是我们最高听到的最大的数了。美国宇航局NASA在它的一篇科目系列Ask Us中,曾认真的回答了这个问题(虽然没有给出具体的数值,但大概是1后面几十个0)。而最微小的呢,也许是大学物理我们学到的普朗克常量,它的值是:
也不过是小数点后面34个零而已,光是这点浮点数就能穷尽宇宙之浩瀚、之微渺,那我们有完全有理由相信64 bit表示的浮点数已经足够我们用了。
既然所能表示出来的浮点数集合是有限的,那么好钢要用在刀刃上,我们必须要选择将常用的浮点数(精度)都能尽可能精确的表示出来,而对于其他浮点数值,则可以通过舍入的办法来表示。
4.2 为什么选用浮点数而不是定点数表示实数呢?
先说结论,目前计算机系统采用的浮点数表示都是1980s前后制定的IEEE 754标准。再说为什么:
定点数表示
和整数相比,实数多了小数部分,也就是小数点之后还有值,因此,对于给定的w位表示的浮点数,我们还要拿出一定的位数s来表示小数,这是基本思路。按照这个思路我们一个最直接的方案就是比如对于16位的存储空间,我们选用后7位作为小数部分,以小数点为原点,每左移一位,其权重就翻倍,每右移一位,其权重就降50%(也即除以2)。如lihux.me-14所示:
为了表示正实数和负实数,我们选择小数点左边的整数部分采用补码表示,因此我们很容易得到4 bits所能表示的整数范围是$[-8,7]$。而小数点右边表示的小数范围是:$[0/16, 1/16, 2/16, …, 15/16]$,因此我们得到8 bits定点表示的实数范围是:$[-8,7].[0/16, 1/16, 2/16, …, 15/16]$,共计$16 * 16 = 256$个浮点数。为了对这些点的分布有一个直观的理解,我在自己的Demo App中将这些点给画出来了:
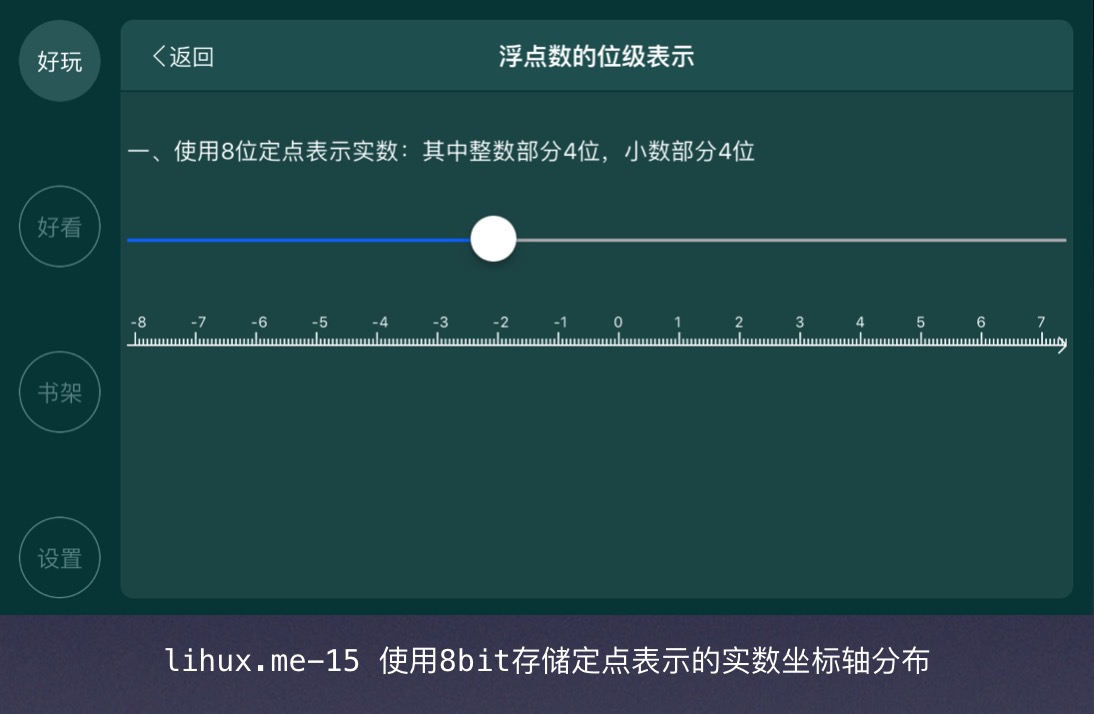
从图中可以看到,这些点均匀分布,看上去很完美。那么下面我们来看看浮点表示:
概况而言,浮点数的表示的基本公式如下:
其中:
- 符号
s (short for sign)决定表示的是正数(s=0)还是负数(s=1),因此要占用1 bit; - 尾数
M,尾数significand是一个二进制小数,它的范围是$1\sim2-\varepsilon$(规格化),或者是$0\sim1-\varepsilon$(非规格化);
-阶码E (short for Exponent)的作用是对浮点数加权,权重是2的E次幂(可能是负数);
也就是说浮点数需要存储三个值:s/M/E 。看定义觉得很难懂,还是来点儿例子吧:我们以32 bit长度的单精度浮点数的表示为例来说明这一点:
图中可以看出,s/M/E三部分占用的位数分别是1、8和23,除了符号位需要固定1 bit之外, 尾数和阶码占用的位数实际上是根据实际需要自己定义的,这里因为我们通常对精度要求非常高,而对极大数的表示的要求有相对比较低,所以尾数表示占用的位数是阶码的三倍。
而这里令人不愉快的是常规数的表示还分为规格化和非规格化两种,原因就是我们对精度要求的贪婪:在浮点数表示中,二进制的小数部分,第一位一定是1(要么是0要么是1),既然一定会有1的存在,那么我们就没有必要存储了,将其省掉,这样就等于后面又能多存储一位尾数!
这里的阶码表示采用无符号数表示,但因为无符号表示的数只能是$0\sim255$,因此对于规格化的阶码部分的无符号数表示的值会在$1\sim254$之间,但我们还需要负数以表示绝对值极小的数,因此我们对这个值再减去一个常量$2^7 - 1$,也就是127,因此阶码的实际范围是$-126\sim127$。让我们继续用公式简单的总结一下对于w位表示的阶码值的计算我们有:
其中e为无符号表示的阶码的值,Bias为偏移量。
规格化的浮点数表示虽然帮助贪婪的我们多表示了1位精度,但是却带来了另外一个尴尬的问题:由于我们贪婪的添加了一个无形的1(让我想起了经济学中的无形的手了^_^),就导致尾数部分永远不为零,这些完蛋了:我们没法表示零了!!!
别急,我们的计算机科学家们并没有被这个困难所吓到,他们想了想,既然这样,那干脆在阶码为0的时候,我就不加那个无形的1了呗!但是呢,因为去掉了那个无形的1,其实是等价于我们的阶码值在规格化的基础上进行了减1($2^{-1}$),那么为了保证在数值表示上,规格化到非规格化的平滑过渡,我们需要对阶码的计算公式人为的做一下调整,以对冲我们拿掉无形的1之后的阶码值的跳变,因此对于w位的非规格化的阶码值的计算我们有:
ok,浮点数的定义现在我们彻底搞清楚了,这里的浮(float)的意义我们也清楚了:就是相对于定点数的表示,浮点数通过阶码的值的变化来达到小数点的浮动的效果,而不是我们的尾码或者阶码本身表示的位数变动的意思。
如果不出意外的话,我们现在应该只剩下最后一个问题了:为什么选用浮点表示而不是定点表示呢?答案是浮点数表示更能贴服我们的需求:对于我们经常使用的实数范围进行更高密度的表达,而不是像定点数那个一视同仁,我们仍在Demo中看看,既然是要对比着找答案,那么我们就将8 bit长度的定点数和浮点数放在一起同时绘制出来,让我们来看看他们有什么不同:
很容易我们就发现了两点:
- 浮点数表示的实数范围更小;
- 浮点数表示的实数集合分布不均匀,越靠近零点,分布的越密集;
关于上述两点,我们可以通过设置不同的二进制位数来确认这不是一种偶然:
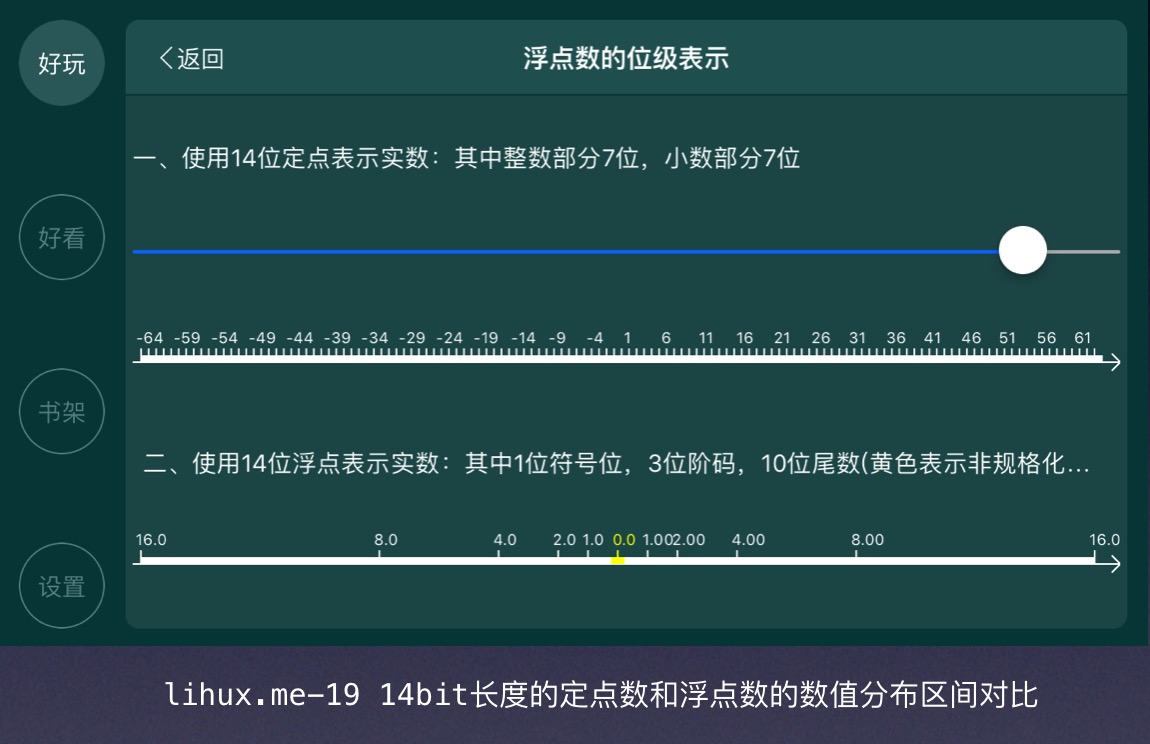
浮点数的分布不均匀的特性正式我们选择它的一个重要原因:既然实数是一个无穷集合,而我们的计算机资源是有限的,那么就必须要将好钢用在刀刃上:对于表示的范围不必那么大,够用就行;对于表示范围内常用的数值区间,我们提供更高的精度(尾数更长)来表示。
好了,关于浮点数这一步分就先到这里,关于浮点数的计算就先不做展开了,不然本文的长度恐怕是有点吓人了。
5.0 小结
没想到关于第二章的读书笔记会写这么长,也许是觉得信息的表示是计算机系统中基础的基础吧。本文通过19副图和一个APP Demo,强大的资源集合以及10个左右的数学公式,力图将信息在计算机系统的表示给讲清楚。
计算机将信息编码为位(比特 or bit),通常组织成字节序列。所有的整数、实数和字符串都通过这样一位位01字符串来表示,要想解析出其中所表示的信息,我们必须要按照预先约定好的解码规则进行解码。而本篇基本围绕着基本数据类型的编码规则来进行讲解:编码的方式(函数)以及为什么选用某一个编码方式而不选用另外一种方式。通过数学分析以及编写程序,从理论上和实际使用中找出原因,以期给自己也给本文的读者一个令人信服的答案。